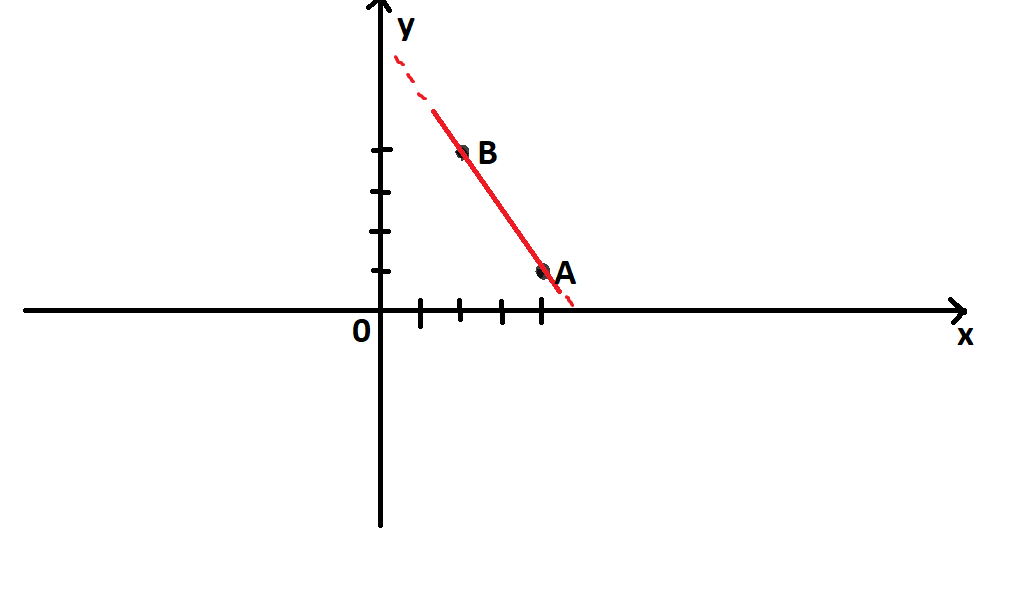
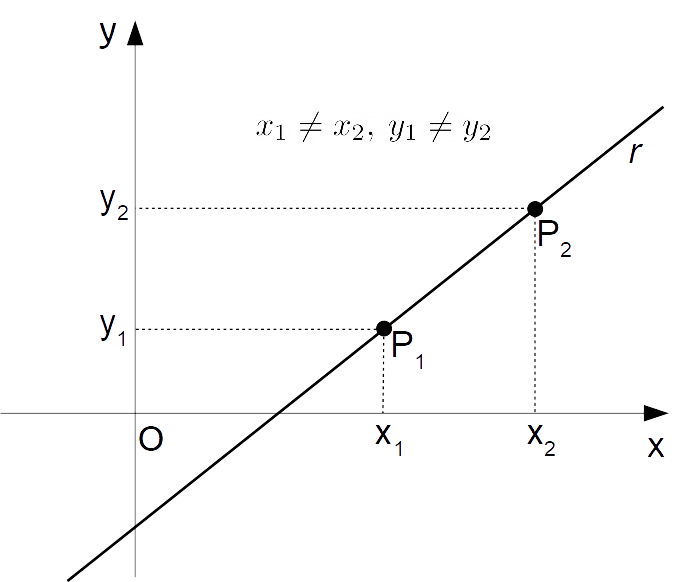
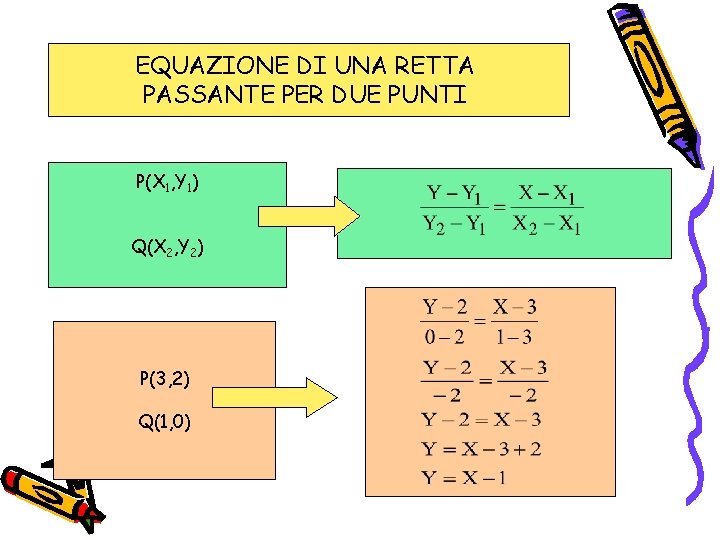
Consideriamo due punti generici, P ( x 1; y 1) e Q ( x 2; y 2), e determiniamo l'equazione della retta passante per essi. y − y 1 = m ( x − x 1) in cui m assume un certo valore che ora determineremo. Questa è l'equazione della retta passante per i punti dati. ESEMPIO. Applichiamo la formula appena ricavata per determinare l'equazione.. L'equazione della retta passante per i due punti è data da: x = x_1 x = x1. oppure, il che è lo stesso: x=x_2 x = x2. Non è possibile in questo caso calcolare il coefficiente angolare, in quanto i due punti hanno la stessa ascissa e di conseguenza nell'espressione del coefficiente angolare:

Retta per due punti YouTube

La retta passante per uno e due punti Andrea il Matematico

L'equazione della retta nel piano cartesiano YouTube
L'Equazione di una retta passante per due punti Blog didattico

Equazione della Retta Passante per Due Punti YouTube

La retta passante per uno e due punti Andrea il Matematico

La retta passante per uno e due punti Andrea il Matematico

MappeDSA EQUAZIONE DELLA RETTA PASSANTE PER L'ORIGINE DEGLI... Equazione, Matematica scuola

Equazione della retta passante per un punto matematicaoggi
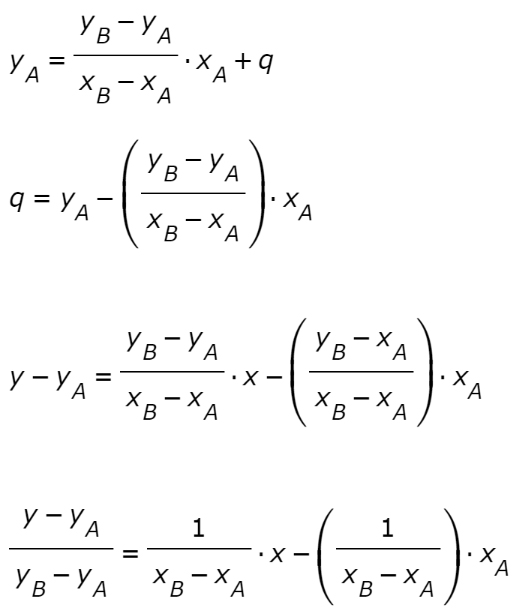
Retta passante per due punti la formula completa con esercizi svolti
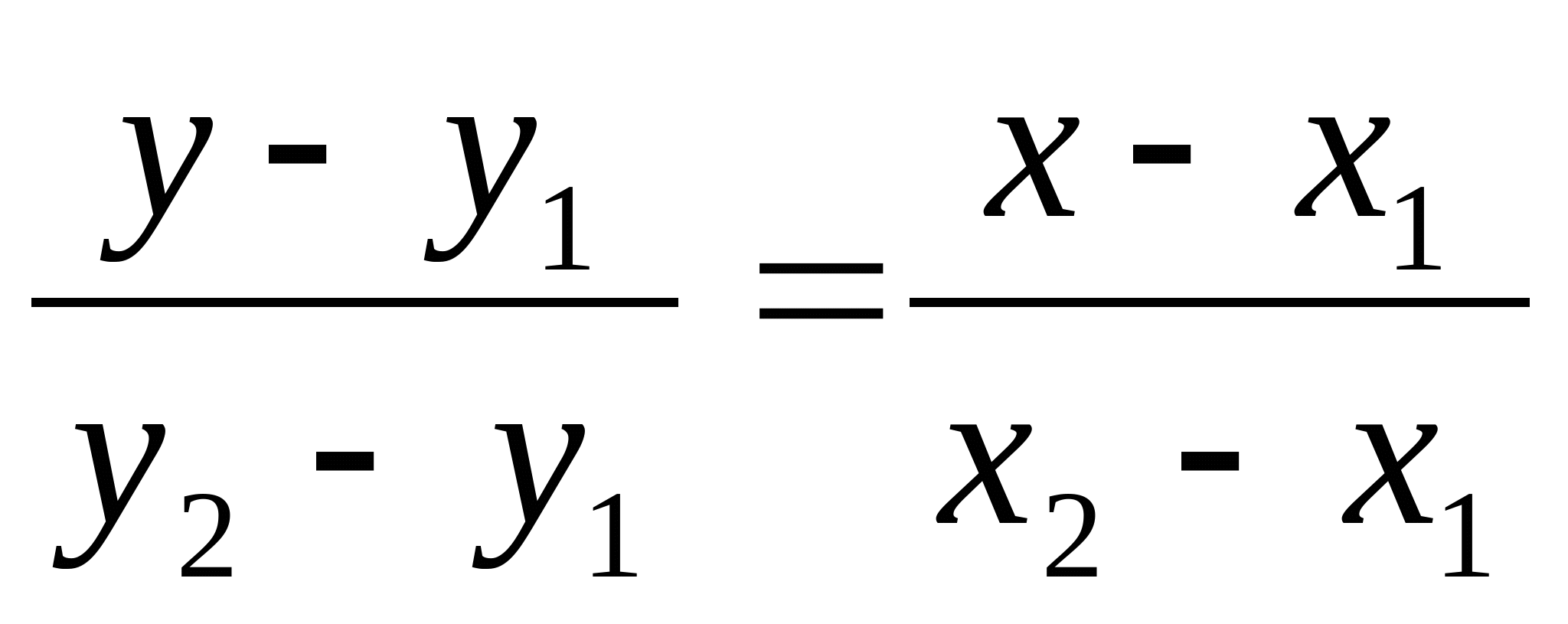
RETTA PASSANTE PER DUE PUNTI Qual è lo

La retta passante per due punti Infodit

Equazione Retta passante per due Punti esercizio 5 YouTube
Retta passante per due punti SìMatematica

📐💻 Equazione di una retta passante per due punti guida pratica con esempi e formule YouTube

EQUAZIONE GENERALE DELLA RETTA lezioniignoranti
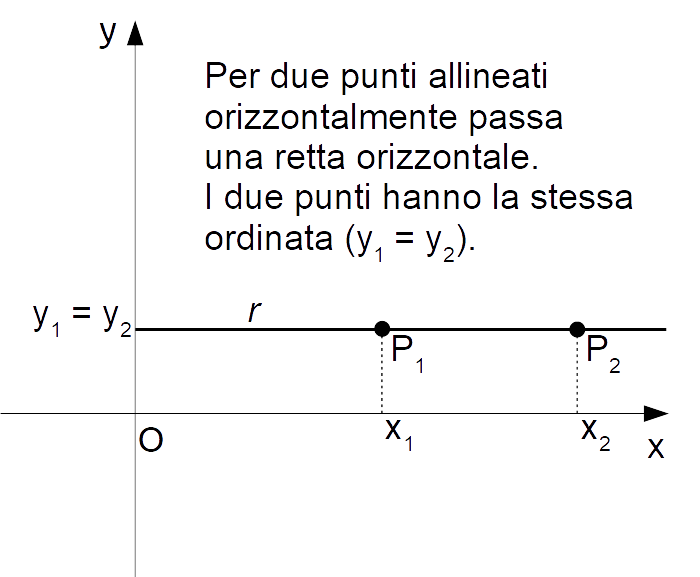
Retta passante per due punti SìMatematica

La retta passante per uno e due punti Andrea il Matematico

La retta passante per uno e due punti Andrea il Matematico
Il piano cartesiano e la retta Mappe schemi
La retta passante per i due punti P 2 e P 1 equivale al seguente vettore direttore P 2 P 1:. Ho così determinato la formula dell'equazione generale della retta passante tra due punti. La dimostrazione finisce qui. Un esempio pratico. Dati due punti del piano P 1 e P 2 $$ P_1 \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = P_1 \begin{pmatrix} 7.. condizione di parallelismo tra le due rette. condizione di perpendicolarità tra le due rette. equazione cartesiana in forma esplicita (canonica): coefficiente angolare : termine noto o intercetta o quota: equazione della retta passante per due punti. x=x 1 se x 2 =x 1. y=y 1 se y 2 =y 1. equazione della retta passante per un punto.